私が現在勉強しながら研究している非線形性に関する理論を簡単にまとめておきます．

もちろん，まだ一回も発表もしていない研究の内容をそのまま書くのはさすがにいけないので，ここではすでに世間ではよく知られているような内容のみをまとめておきます．

表記について

• \(j\)：虚数単位
• \(\mathcal{F}[\cdot]\)：フーリエ変換

ここで，\(S(f)\)を\(s(t)\)のスペクトル，\(\left\lvert S(f) \right\rvert^2\)を電力スペクトル密度とそれぞれ呼びます．

• \(\delta(x)\)：ディラックのデルタ関数

• \(\text{sinc}(x)=\frac{\sin \pi x}{\pi x}\)：sinc関数

正弦波のフーリエ級数展開

まず，フーリエ変換について復習しておきます． 正弦波は周期関数なので，正弦波のフーリエ変換（スペクトル）はフーリエ級数に展開したときの係数で表せます．

ここで，周期\(T_0 = \frac{1}{f_0}\)の任意の信号\(s(t)\)の複素フーリエ係数が\(c_n\)であれば，\(s(t)\)のスペクトルは次のように表せます．

そのため，まずは複素フーリエ係数\(c_n\)を求めてみます． ここで，\(c_n\)とは複素正弦波\(e^{j 2 \pi n f_0 t }\)と信号\(s(t)\)の内積で計算されます．

\(s(t)=e^{j2\pi f_0 t}\)のとき，\(c_1=1\)で\(c_{n\not=1}=0\)になりますね？

では，話を戻して正弦波，つまり\(s(t)=\cos(2\pi f_0 t)\)のときにはどうなるでしょうか？ ここでは，オイラーの公式より

になることから直ちに

がわかります． つまり，正弦波のフーリエ変換はは次のようになります．

グラフで表すと以下の図のようになります． ここでは，ディラックのデルタ関数を表現するために矢印を用いて，その高さを係数\(c_n\)にしています．

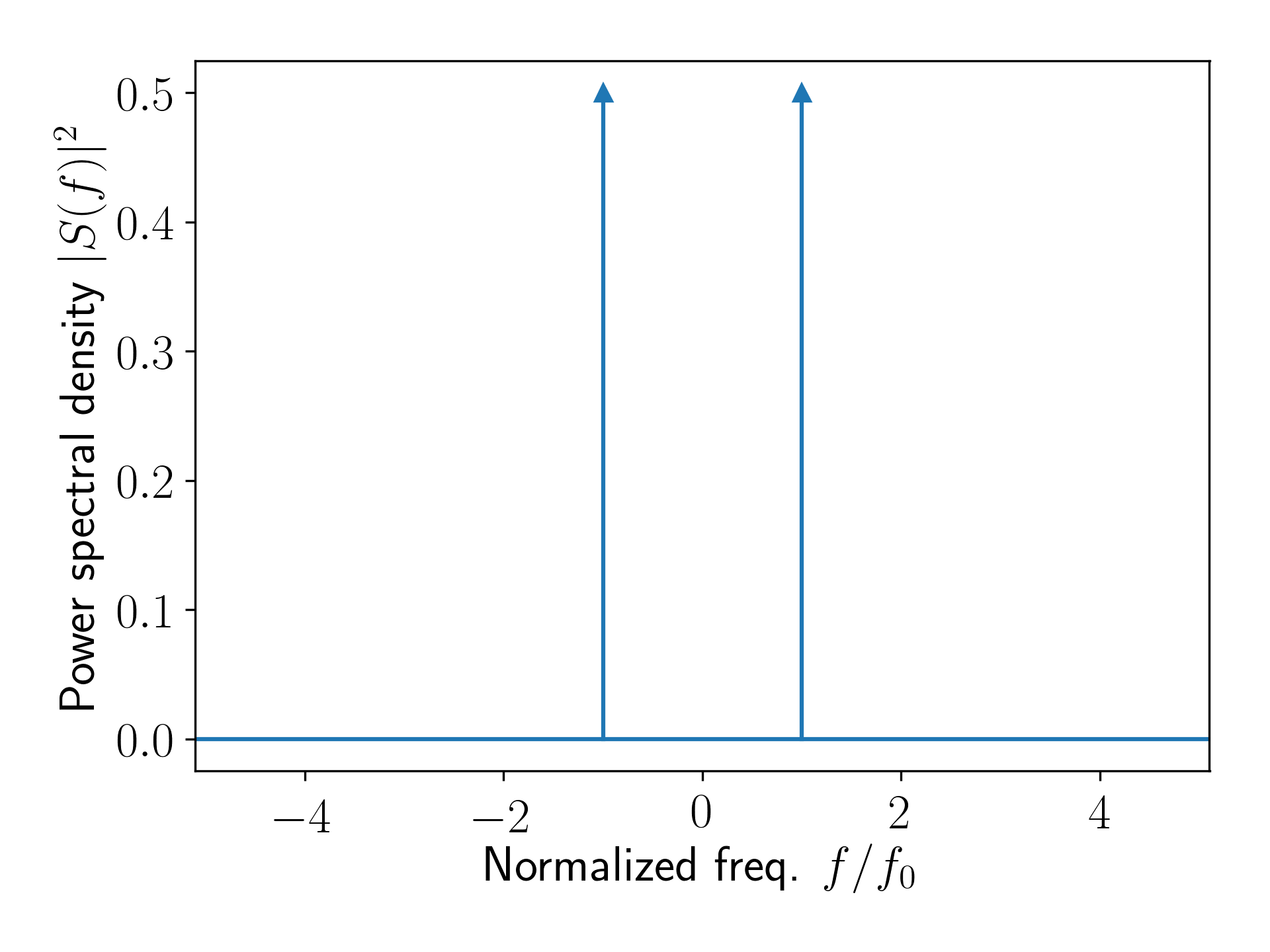
矩形波のスペクトル

次に，よくある矩形波のスペクトルを考えてみます． ここでは周期\(T_0=\frac{1}{f_0}\)の次のような矩形波\(r(t)\)を考えます．

ただし，上の式の定義外については\(r(t)\)が周期\(T_0=\frac{1}{f_0}\)の周期関数となるように定義します．

この矩形波は\(0\)を中心に半分の区間では\(1\)に，残り半分の区間では\(-1\)になっています．

この矩形波のスペクトルを調べるために，まずは複素フーリエ係数を調べます． \(r(t)\)が偶関数であることに注目すると，

\(n\not=0\)においては

を得ます． また，\(n=0\)では\(c_0=0\)です． そのため，矩形波のスペクトルは

となります．

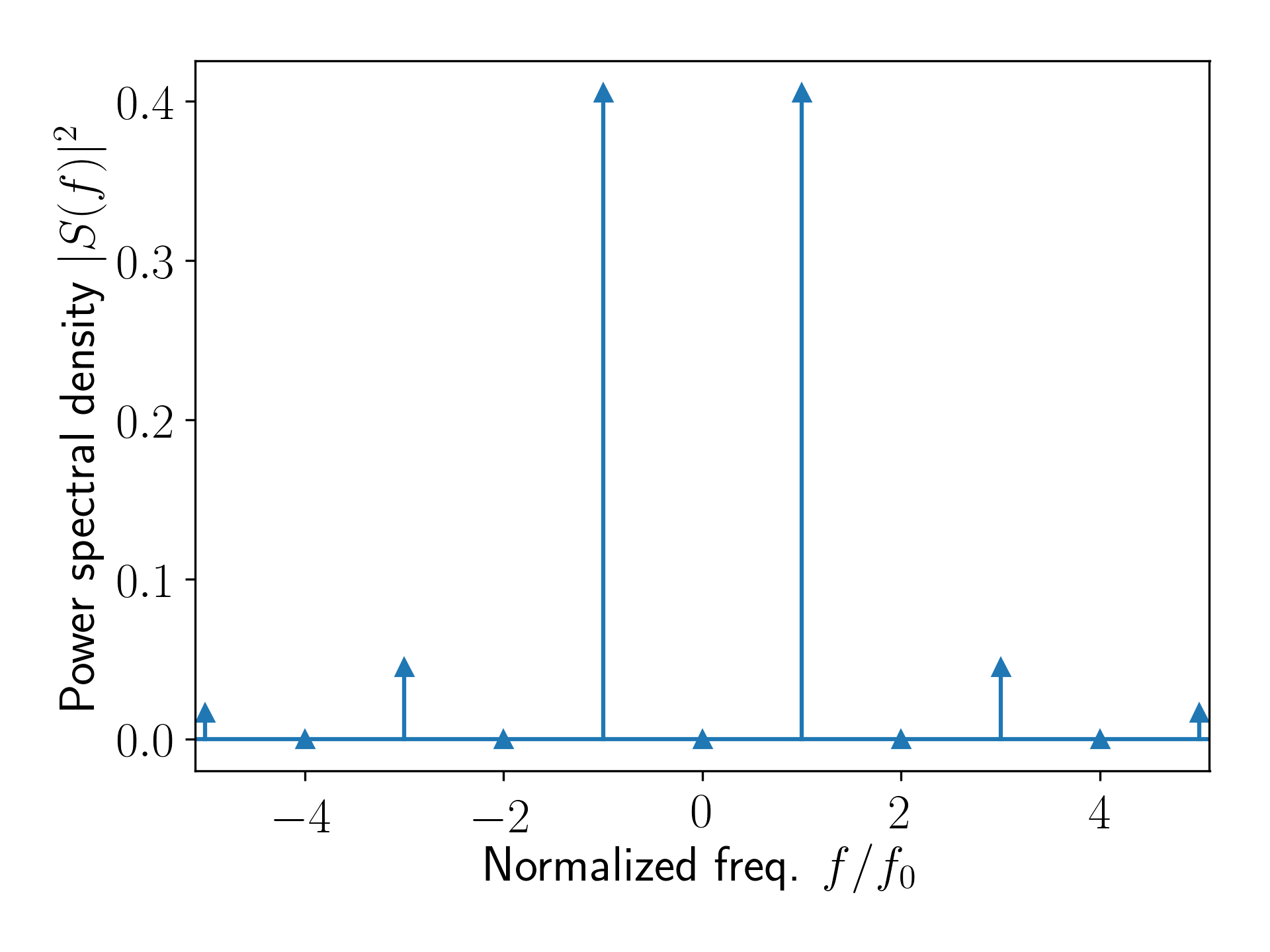
非線形変換を受けた正弦波

ここで，次のような非線形関数を考えます．

この非線形関数\(g(x)\)は\(x\)が少しでも正に値を取れば\(1\)に，少しでも負に値を取れば\(-1\)に，\(0\)であれば\(0\)になるような関数です．

この関数は矩形波の定義に似ているかもしれませんが，周期関数ではありません．

この非線形関数を用いて矩形関数は次のように定義できます．

これを周波数領域で考えてみると，正弦波の2本の線スペクトルは\(g(x)\)な非線形特性を有するシステムを通過することで無限個の線スペクトルに化ける，と考えられます．

では，任意の非線形関数が与えられたとき，その非線形関数のどのような特徴が出力のスペクトルを決定づけるのでしょうか？

つまり，\(g(x)\)の特性だけがわかっているときに，正弦波を実際に適用することなくその出力のスペクトルを予想することはできるのでしょうか？

チェビシェフ多項式による展開

この問に関する答えは，意外かもしれませんが，チェビシェフ多項式という直交多項式にあります．

実は，任意の関数\(g(x)\)をチェビシェフ多項式\(T_k(x)\)で展開したときの係数と，\(g(\cos(2\pi f_0 t))\)のスペクトルにはある関係があります．

ここで，チェビシェフ多項式\(T_k(x)\)とは\(m\not=n\)において次の関係を満たすものです．

具体的には

となっています． また，面白い特性として

となります．

このチェビシェフ多項式を用いて\(g(\cos(2\pi f_0 t))\)のスペクトルは次のように記述できます．

なぜこんなことをするのでしょうか？

それは，\(a_n\)の積分で\(x=\cos(2\pi f_0 t)\)と置換積分することでわかります．

\(\frac{dx}{dt} = -2\pi f_0 \sin(2\pi f_0 t)\) で積分区間は\(\frac{1}{2f_0} \rightarrow 0\)です． また，\(dx/\sqrt{1-x^2} = -2\pi f_0 dt\)になるので，

となります． よく観察してみれば，これは複素フーリエ係数\(c_n\)そのものだということがわかります．

ん？じゃあこれは単に複素フーリエ係数を求める積分を変数変換しただけでは？と思うかもしれません．

そのとおりです！

ですが，もう少し考えていきましょう．

チェビシェフ多項式\(T_n(x)\)と係数\(a_n\)を用いることで，任意の非線形関数\(g(x)\)を表現することができます． つまり，

となる\(a_n\)があります． そしてこの\(a_n\)はフーリエ係数なのです．

何が嬉しいかというと， ある非線形な入出力特性をもつ素子や電気回路の特性をチェビシェフ多項式で近似したいとします．

この素子や回路の入力に正弦波を入れ，素子の出力をフーリエ変換すると，その係数が素子をチェビシェフ多項式で近似したときの係数になる，というのです！

さらに，逆も成り立ちます． チェビシェフ多項式を用いて特性が近似されたある素子に正弦波を入れたときの出力信号のフーリエ係数はチェビシェフ多項式の係数なのです．

最後に

以上までは，入力信号を正弦波にしたときの結果を述べました． ここではもう少し拡張してみて，入力信号が逆正弦分布という確率分布に従う場合を考えてみます． この逆正弦分布の確率密度関数は

となります． \(\theta \sim U(0,2\pi)\)のとき\(\sin \theta\)，や\(\cos \theta\)は逆正弦分布に従います．

\(a_n\)を求めるときに用いた積分は，実は逆正弦分布に従う入力信号\(x\)について\(\mathbb{E}[g(x)T_n(x)]\)を求めていただなのです． そして，逆正弦分布に従う入力信号についてはチェビシェフ多項式が直交多項式となり，その係数はスペクトルと面白い関係を持ちます．

Rust入門３日目のけーさんです．

Rustを使ってスタックを実装したいとき， 再帰的データ構造を意識すれば，次のようにスタックを実装できると思います．

struct Stack<T> {
    head: Option<Box<Node<T>>>
}

struct Node<T> {
    elem: T,
    next: Option<Box<Node<T>>>
}

impl<T> Stack<T> {
    pub fn new() -> Self {
        Stack { head: None }
    }

    pub fn pop(&mut self) -> Option<T> {
        // ...省略
    }

    pub fn push(&mut self, e: T) {
        // ...省略
    }
}

このStack<T>はもちろんちゃんと次のテストが通ります． （そのようにpush, popを実装します）

let mut stack = Stack::new();

assert_eq!(stack.pop(), None);

stack.push(123);
assert_eq!(stack.pop(), Some(123));

stack.push(1);
stack.push(2);
stack.push(3);
assert_eq!(stack.pop(), Some(3));
assert_eq!(stack.pop(), Some(2));
assert_eq!(stack.pop(), Some(1));
assert_eq!(stack.pop(), None);

しかし，次のコードはfatal runtime error: stack overflowでプログラムが異常終了してしまいます．

let mut stack = Stack::new();

for i in 0..20_000 {
    stack.push(i)
}

たったこれだけのコードで，このStackの何がいけないのでしょうか？ 結論からいえば，タイトルにもある通りデストラクタが原因です． この場合はstackのデストラクタの呼び出しを皮切りに，再帰的にNodeのデストラクタが呼び出されることでスタックオーバーフローになります．

もう少し噛み砕くと，まずstackのデストラクタが行われますが，stackのデストラクタの内部ではstack.headのデストラクタが行われます． 同様にstack.headのデストラクタではstack.head.elemとstack.head.nextがデストラクタが実行されますが，stack.head.next.nextも．．．というように再帰的にデストラクタが実行されるのです．

この問題はStackに数個要素を追加するだけでは発生しませんが，しかし2万個程度要素があるだけでデストラクタはスタック領域を食いつぶしてしまうのです．

僕がこの問題に直面したとき，なぜスタックオーバーフローとなっているのか全く理解が出来ませんでした．

この問題に気づきにくい原因は２つあると思います．

• この問題は再帰的なデータ構造に特有な問題
• デストラクタがコードに表れておらず，動作が読み取りにくい

特に2つ目が主な原因だと思います． C++やD言語でもそうですが，構造体のデストラクタはコンパイラが自動的に生成してくれるので，プログラマがわざわざ自分で書く必要がない場合が多いと思います．

しかし，再帰的なデータ構造ではこのデフォルトのデストラクタが悪さをしてプログラムをスタックオーバーフローへと導きます．

この問題はRustのみの問題ではなく，C++でも同様に起こります．

template <typename T>
struct StackNode {
    StackNode(T e, std::unique_ptr<StackNode<T>> && n)
    : elem(e), next(std::move(n)) {}

    T elem;
    std::unique_ptr<StackNode<T>> next;
};

template <typename T>
struct Stack {
    std::unique_ptr<StackNode<T>> head;

    void push(T elem) { /* ...*/ }
};

int main() {
    Stack<int> stack{};
    for(int i = 0; i < 1000000; ++i) {
        stack.push(i);
    }
}

対策

自分でちゃんとデストラクタ，つまりRustではDropトレイトのdropを実装すれば問題は起こりません．

impl<T> Drop for List<T> {
    fn drop(&mut self) {
        let mut node = mem::replace(&mut self.head, None);

        while let Some(x) = node {
            node = x.next;
        }
    }
}

C++でも同じです．

template <typename T>
Stack<T>::~Stack()
{
    while(head) {
        auto h = std::move(head);
        head = std::move(h->next);
    }
}

はじめに

この記事は、TUT Advent Calendarの22日目の記事であり、さらにD言語 Advent Calendarの23日目の記事です。

私は某国立大学の大学院の電気・電子情報系学科に所属していて、来年からは博士課程に進学する予定です。 研究の分野は無線通信で、特に「全二重通信」と呼ばれる次世代の無線通信方式についてディジタル信号処理の観点から研究しています。

今回の記事では、私が今年一年間で研究室にてD言語で作った成果について紹介します。

ベースバンド信号シミュレータ

無現在のディジタル線通信は数百MHzから数GHz以上の周波数の電波を使用します。 この電波に載せる信号をシミュレーションするソフトウェアをベースバンド信号シミュレータといいます。 オープンソースのベースバンド信号シミュレータ系ライブラリのといえば、GNU RadioやIT++が有名だと思います。 しかし、GNU Radioは拡張性が良いとは言えず、IT++はここ数年全く保守されていません。 あと、GNU RadioはPythonかC++で、IT++はC++で記述できますが、やっぱりD言語で研究したいです。 ということで、ベースバンド信号シミュレータ系ライブラリをD言語で作りました。 論文の関係上まだGitHubにはソースコードを上げていませんが、現在IEEE Trans. on Wireless Communicationsに出している論文がAcceptされ次第ソースコードの公開をします。 ちなみに、このライブラリを使用してシミュレーションした結果は2017年3月にサンフランシスコで開催された国際会議IEEE WCNC (Wireless Communications and Networking Conference)にて発表しました。 そのときの会議論文はこちら（ちゃんと論文中にシミュレータがD言語製であると記述しています！）。

ソフトウェア無線（USRP）用ライブラリ

リポジトリはこちら

こちらも無線通信関係です。 USRPというソフトウェア無線用RFフロントエンド用のD言語ライブラリを作りました。 ソフトウェア無線とは、ソフトウェアによってベースバンド信号処理を行い、その信号を電波に載せたり、逆に電波をベースバンド信号に変換しソフトウェアで受信処理を行う無線機です。 USRPはソフトウェアによって作られたベースバンド信号を電波に載せたり、電波からベースバンド信号に変換する装置で、一つ20万円から100万円くらいします。 USRPはGNU RadioやUHDというC++用のライブラリを用いて制御でき、実際に弊研究室では従来までこれらを利用してC++で書かれたソフトウェアでベースバンド信号を生成したり、受信処理を記述していましたが、コードが煩雑になってしまってました。

やっぱりD言語でソフトウェア無線できると嬉しいので、研究の合間にちまちまコードを書いていました。 このライブラリでは、UHDが公開しているC言語用APIを利用して、UHDよりも扱いやすいように作っています。 このライブラリはすでにGitHubにて公開しています。

また、このライブラリを用いて実際にUSRPを3台制御するデモを2017年11月29,30日、12月1日の3日間開催されたマイクロウェーブ展にて展示してきました。 当日の様子はこんな感じです。

実機の展示はこんな感じです。D言語で書かれたソフトウェアで信号処理をして無線機から高周波信号を出しています #dlang pic.twitter.com/LhyuYYm0L4

— けーさん@緊急復活 (@k3k0ma) 2017年11月29日

クラスタ計算機用ジョブ投入ライブラリ

リポジトリはこちら

豊橋技術科学大学には10コアのXeonが二つ載ったノードが30ノード繋がったクラスタ計算機が設置されており、学生が研究や学習用途に自由に利用することができます。 私も最近ではシミュレーション条件をたくさん振ったり、乱数のシードを変えて試行回数をたくさん稼いでシミュレーションをしているので、どうしてもクラスタ計算機のようなHPC環境がないとシミュレーション時間がかかってしまいます。

しかし、クラスタ計算機のジョブスケジューラにジョブを投げるために投入用スクリプトを書かないといけないのが少しめんどくさいです。 たとえば、変数tを1から100まで変えてプログラムprogを走らせるジョブの投入スクリプトは次のような感じになります。

#PBS -l nodes=1:ppn=1
#PBS -t 1-100
#PBS -q wLrchq

cd $PBS_O_WORKDIR
./prog ${PBS_ARRAYID}

このように、ジョブスケジューラの機能だけだと、イテレートする変数が整数一つだけで、たとえばforeach(e1; param1) foreach(e2; param2) {...}のように複数パラメータを総当りしてシミュレーションすることも簡単にはできません。 また、同じソースコードで、手元のPC上ではCPU個数分だけ並列動作し、クラスタ計算機では複数ノードで並列処理されるようなコードを書くのも困難でしょう。

私が作ったクラスタ計算機用ジョブ投入ライブラリでは、以下のような感じで簡単にD言語からジョブ投入できます。

import std.stdio;
import tuthpc.taskqueue;

void main()
{
    JobEnvironment env;
    auto list = new MultiTaskList();

    // 2変数を総当りして256個のジョブ生成
    foreach(i; 0 .. 16)
        foreach(j; 0 .. 16)
            list.append!writefln("Hello, TUTHPCLib4D! %s", i);

    // クラスタ計算機で動かすとジョブ投入、それ以外では並列実行
    run(list, env);
}

実行もパッケージマネージャdubを使えばdubだけで、ローカルでもクラスタ計算機でも動きます。 また、クラスタ計算機上のN個のノードで各M個のコアを専有したい場合にはdub -- --th:g=M --th:m=Nと実行すればその通りにジョブ投入されます。

また、C言語から扱う場合やC++から扱う場合のサンプルコードもリポジトリに添付しています。 このライブラリはわりと便利で実用的なので技科大生でクラスタ計算機利用している人にはおすすめです。

まとめ

振り返ってみると、2017年はわりといろいろと作ってた感じでした。 来年にはこの記事の最初に紹介したシミュレータ用のライブラリも公開できると思いますので、そのときにはまた記事を書きたいと思います。

突然今週初めに，研究のソースコードを管理しているGitリポジトリが壊れてしまったので， 一部始終をまとめておきます．

dubで提供されているロックフリーなパッケージlock-freeのベンチマークを取ってみました．

前のリポジトリが非常に扱いづらかったので新しく移行しました．